Ідеї ☝
TED-ED : шикарний канал логічних задач
Шикарний канал з логічними задачами ще й англійською мовою
TED-ED https://www.youtube.com/channel/UCsooa4yRKGN_zEE8iknghZA /
TED-ED : цікаві задачі для захоплених логікою та англійською. Хоча з українськими титрами є теж купа задач... Прекрасні вкраплення в білінгвальні уроки чи для занять у студіях логіки
Навіщо вивчати математику?
Чому математика «рулить»
Що ми втрачаємо при навчанні учнів у школі. На що варто звернути увагу, щоб наші першокурсники були більш успішними?
Хвиля "Вежі" ( матеріали будуть)
 Класний сервіс, круті візуалізації та вправи!
Класний сервіс, круті візуалізації та вправи!
Просто відео про маркування футбольного поля. ⚽ Розібратися у зонах футбольного поля, легко нанести маркування на масштабований макет, натренувати себе обчислювати периметри і площі прямокутників і, навіть, спробувати обчислити площу та довжину кола - все це можливо реалізувати на уроці математики побудованому на основі цього відео. І вже у 5 класі! Мабуть , все таки зачекаю, поки вивчемо десяткові дроби!

👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈
- Проста математика: 13 уроків від спікерів TED- 12 фактів про математику та цікаві наукові знахідки - TED-ed - Pinterest : дошка MATH , дошка У ШКОЛІ ЗНАДОБИТЬСЯ
👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉👉
Доведення площі круга так, як це робив Архімед
Розв'язування квадратних рівнянь методом Аль-Хорезмі 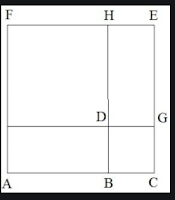
👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍👍
https://www.facebook.com/oxana.fils/videos/2175373419164717/UzpfSTEwMDAxNDIwMjE1MjU0OTo2OTcyMzE0MDc0MjY5MjU/
МЕГА круті командні ігри🏃🎎🏀🎉🎈
МЕГА круті командні ігри🏃🎎🏀🎉🎈
!!! ПЕРШИЙ УРОК - напрацювання ПРАВИЛ і СПІЛЬНОГО бачення процесу навчання, ДОМОВЛЕНОСТІ -відповідно до правил школи Саммерхіл???
Урок однієї задачі: напрацювання ідей, обмін ідеями, вибір ідей!
👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐👐
Швидкість і продуктивність праці: юнаки на смартфонах набирають тексти різної довжини. Хто швидше? Той, хто раніше закінчив чи той, у кого продуктивність праці більша ???
Три чоловіки сидять за столами із попкорном. У одного 10 шт. розсипано на столі, а інші у стакані. У другого- 25 шт. розсипано, інші у стакані. У третього- всі у стакані. Таймер вмикають тоді, коли чоловіки сідають за стіл. Аналізуємо кількість і швижкість з'їденого попкорну за певний час.
Ідея: http://www.insidemathematics.org/
БЛОГ "Ілюстративна математика" - гарні ідеї та рекомендації. Правда англомовний... Навіть є розроблені уроки... Цікаві компетентнісні завдання, наприклад
БЛОГ "Ілюстративна математика" - гарні ідеї та рекомендації. Правда англомовний... Навіть є розроблені уроки... Цікаві компетентнісні завдання, наприклад
👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈👈
Ідеї з книги "Як ніколи не помилятися. Сила математичного мислення" Джордан Елленберг
1. Запитання: "Навіщо вчити математику?"
Відповідь від автора:«Математика — це не просто послідовність обчислень, які потрібно зубрити, поки у вас забракне терпіння чи сил — хоча, можливо, саме так вас учили в курсі математики. Ці інтеграли для математики — як силові вправи і загальна фізична підготовка для футболу. Якщо ви хочете грати у футбол — маю на увазі справді грати, на рівні змагань, — потрібно робити багато нудних, однакових, начебто безглуздих вправ. Чи використовують коли-небудь професійні гравці ці тренувальні вправи? Ну, ви ніколи не побачите на полі гравця, що тягне гантелі чи оббігає конуси. Але ви побачите, як гравці використовують силу, швидкість, реакцію і гнучкість, які вони випрацювали цими тренуваннями — довгими тижнями виснажливих тренувань тренувань. Ці вправи — підготовка до футболу.
Якщо ви хочете заробляти футболом на життя чи навіть просто грати в університетській команді, вам доведеться віддати багато вихідних нудним тренуванням. По-іншому не вийде. Але є й добра новина. Якщо так тренуватися — це для вас занадто, ви все одно зможете грати у футбол для задоволення, із друзями. Ви зможете радіти вправному пасу між захисниками або результативному удару з далекої відстані, доступним тільки справжнім спортсменам. Ви будете здоровішим і щасливішим, ніж якби просто сиділи вдома і дивилися гру професіоналів по телевізору.
Математика — багато в чому те саме. Ви можете не мати на меті отримати роботу, пов’язану з математикою. Це нормально — більшість людей не мають такої мети. Але ви можете займатися математикою. Ймовірно ви вже займаєтеся математикою, навіть якщо цього не усвідомлюєте. Математика вплетена у те, як ми мислимо. І математика вам допомагає. Знати математику — це як надягти рентгенівські окуляри, які відкривають структуру, приховану за незугарною й хаотичною поверхнею світу. Математика — це наука не помилятися, її прийоми і методи віками виковувалися тяжкою працею і запеклими суперечками. Маючи під рукою математичний інструментарій, ви зможете розуміти світ глибше і краще. Усе, що потрібно — це тренер чи просто книжка, які навчать вас правил і головних прийомів. Я буду тренером."
ПРИКЛАД ІЗ ЖИТТЯ ПРО НЕОБХІДНІСТЬ МАТЕМАТИЧНОГО МИСЛЕННЯ
Абрагам Вальд і відсутні кульові пробоїни
Ця історія, як і багато історій періоду Другої світової війни, починається з переслідування нацистами єврея, а закінчується тим, що їм це обертається на гірше.
Група статистичних досліджень (ГСД)2, у якій Вальд працював більшу частину Другої світової війни, являла собою секретну програму, яка мобілізувала американських статистиків для роботи на війну — щось на зразок Мангеттенського проекту, за винятком того, що тут розробляли бойові рівняння, а не вибухові пристрої. ГСД справді розташовувалася на Мангеттені, у будинку № 401 по 118-й вулиці, на Морніґсайд Гайтс, лише за квартал від Колумбійського університету. Сьогодні тут квартири викладачів університету та кілька приймалень лікарів, але 1943-го це був постійно заклопотаний нервовий центр військової математики. У Групі прикладної математики Колумбійського університету десятки молодих дівчат, схилившись над настільними калькуляторами Маршана, обчислювали формули для оптимальної кривої, рухаючись якою, винищувач найдовше триматиме ворожий літак на прицілі. В іншому приміщенні група дослідників з Принстона розробляла інструкції для стратегічних бомбардувальників. А просто за сусідніми дверима Колумбійське відділення працювало над створенням атомної бомби.
Однак ГСД була найпотужнішою і зрештою найвпливовішою з усіх цих груп. Тут поєднувалися інтелектуальна відкритість і інтенсивна праця академічної установи з відчуттям спільної мети, яке дає тільки велика відповідальність. «Коли ми давали рекомендації, — пише керівник ГСД В. Аллен Волліс, — часто це мало результат. Боєзапас винищувачів за рекомендаціями Джека Вулфовіца1 був укомплектований різними типами боєприпасів, і пілоти могли повернутися або не повернутися. Літаки морської авіації випускали ракети, пальне яких перевірялося за планом вибіркового контролю Ейба Гіршика, і ракети могли вибухнути і зруйнувати наші літаки, а могли уразити цілі»3.
Математичні таланти, задіяні у роботі, відповідали серйозності завдання. За словами Волліса, ГСД була «найвидатнішою групою статистиків усіх часів, і за кількістю, і за якістю»4. Там працював Фредерік Мостеллер, який згодом організує факультет статистики у Гарварді. А ще Леонард Джиммі Севідж, піонер теорії прийняття рішень і великий прихильник наукової дисципліни, яка отримала назву Баєсової статистики2. Часом забігав математик з МІТ Норберт Вінер, творець кібернетики. Це була група, у якій майбутній нобелівський лауреат з економіки з економіки Мілтон Фрідман часто виявлявся четвертою найрозумнішою людиною.
Найрозумнішим із присутніх зазвичай був Абрагам Вальд. Вальда, викладача Аллена Волліса в Колумбійському університеті, у групі вважали таким собі математичним світилом. Він усе ще був «громадянином ворожої держави» і формально не мав допуску до секретних документів, які сам же й готував; у ГСД жартували5, що секретарям наказали виривати в нього з рук кожну сторінку записника, щойно він закінчить на ній писати. Вальд був тут до певної міри несподіваним персонажем. Його вабила абстракція, а не прикладні задачі. Утім очевидним було і його прагнення застосувати свої таланти у боротьбі проти нацистів. А коли потрібно було надати неясній ідеї математичної точності, саме Вальда краще було мати на своєму боці.
Отже, про що йдеться?6 Ви не хочете, щоб ворожі винищувачі збивали ваші літаки, і тому ви їх бронюєте. Але броня робить літак тяжчим, а тяжчі літаки менш маневрені, і їм потрібно більше пального. Надмір броні на літаку — проблема; брак броні на літаку — теж проблема. Оптимальне рішення десь посередині. Причина, з якої ви зібрали групу математиків у нью-йоркській квартирі, — знайти це оптимальне рішення.
Військові прийшли до ГСД із корисними, на їхню думку, даними. Американські літаки поверталися з боїв над Європою, всіяні кульовими пробоїнами. Однак ушкодження не розподілялися рівномірно по корпусу літака. У фюзеляжах пробоїн було більше, у моторних відділеннях менше.
Частина літака
Кількість пробоїн
на квадратний фут
Двигун
1,11
Фюзеляж
1,73
Паливна система
1,55
Решта літака
1,8
Військові вважали, що є можливість для оптимізації: можна отримати той самий захист меншим обсягом броні, якщо зосередити її у місцях, де вона потрібна більше — там, де літаки отримують найбільше ушкоджень. Але скільки саме потрібно броні для цих частин літака? По відповідь вони і прийшли до Вальда. На це питання відповіді вони не отримали.
Вальд сказав, що бронювати частини, де є пробоїни, не потрібно. Бронювати потрібно ті, де пробоїн немає: двигуни.
Ідея Вальда полягала у простому питанні: куди щезають пробоїни, яких бракує? Ті, які були б на всьому корпусі, якби ушкодження розподілялися по ньому рівномірно? Вальд мав цілковиту певність, що знає це. Пробоїни, яких бракувало, були на відсутніх літаках. Причина того, що літаки поверталися з меншою кількістю пробоїн у моторних відділеннях, полягала в тому, що літаки з пробоїнами у двигунах не поверталися. Тоді як велика кількість літаків, що поверталися на аеродроми з порешеченими фюзеляжами, являла собою доказ того, що з пробоїнами у фюзеляжі можна (а тому потрібно) миритися. У післяопераційних палатах госпіталів набагато більше пацієнтів з пробитими кулями ногами, ніж грудьми. Та це не тому, що солдати не отримують поранень у груди, а тому, що ті, кого поранило у груди, до післяопераційної палати не доживають.
Існує старий математичний прийом, що проясняє картину гранично чітко: прирівняти деякі змінні до нуля.
У нашому випадку така змінна — це ймовірність того, що літак, який отримав ураження двигуна, залишається у повітрі. Прирівняти ці змінні до нуля означає, що єдине ураження двигуна гарантовано збиває літак. Як у такому разі виглядатимуть дані? Тоді б були літаки, що повертаються на аеродром із пробоїнами у крилах, фюзеляжі, носі — але без жодної пробоїни у двигуні. Військові аналітики мали два варіанти пояснення цього: або німецькі кулі влучають в усі частини літаків, за винятком однієї, або двигун є місцем стовідсоткової вразливості. Обидва варіанти пояснюють отримані дані, але останнє набагато достовірніше. Бронювати треба там, де пробоїн немає.
Рекомендацію Вальда було швидко втілено в життя; вона використовувалася у військовій авіації під час Корейської і В’єтнамської війн7. Не можу точно сказати, скільки американських літаків було врятовано, проте, поза сумнівом, наступники ГСД у сьогоднішній армії знають це достеменно. Американські військові традиційно дуже добре усвідомлюють одну річ: країни перемагають у війнах не через те, що вони хоробріші або вільніші за супротивника, чи тому, що Бог до них трішечки ласкавіший. Переможці, як правило, — це ті хлопці чиїх літаків збивають на 5 % менше, хто використовує на 5 % менше пального, хто дає на 5 % більше харчів своїй піхоті за 95 % вартості. Цього не побачиш у кінофільмах про війну, але саме з цього робиться війна. І на кожному кроці тут — математика.
Чому Вальд розумів те, чого не розуміли військові, що значно більше за нього знали про війну в повітрі? Усе зводиться до натренованого математикою способу його мислення. Математик завжди запитує: «З яких припущень ви виходите? Чи обґрунтовані вони?». Ще одна перевага Вальда полягала у його схильності до абстракції.
Через такий характер Вальдові було тяжко зосереджуватися на прикладних завданнях, це правда. Він вважав, що подробиці щодо літаків, кулеметів і гармат були зайвими — його погляд проникав безпосередньо до математичної структури, на якій усе тримається. Часом через
такий підхід можна не помітити того, що має значення. Але він також дає змогу бачити спільну основу проблем, які з поверхового погляду здаються цілковито різними. Таким чином виявляється, що ви маєте важливий досвід навіть у тому, де, здається, не маєте жодного.
ЗНИКОМІ ПРИРОЩЕННЯ І НЕПОТРІБНІ СКЛАДНОЩІ
Неприємності древньогрецького філософа Зенона (5 ст. до н.е.) про те, що не можна дійти до кінцевого пункту (ПРОГРЕСІЇ, РЯДИ...) -------- СТОРІНКА 48-
У ВСІХ ОЖИРІННЯ
Жарт про СТАТИСТИКУ: Естрадний комік Юджин Мірман любить говорити: "Я читав, що 100% американців - азіати".
"Але, Юджин, - протестує співрозмовник, - ти не азіат".
І тут ударна репліка, проголошувана з пишною самовпевненістю: "Та я ж читав, що азіат!"
СТОРІНКА 56 -, 63-
ГРА "ХТО КРАЩЕ КИДАЄ МОНЕТИ?"
ТЕОРІЯ ЙМОВІРНОСТІ, СТОРІНКА 70-
БІБЛІЙНИЙ КОД
Хочете знати про Бога? Є математики, які досліджують це питання. СТОРІНКА 91 -, 99 -
БАЛТИМОРСЬКИЙ БІРЖОВИЙ БРОКЕР
Про те, чи варто довіряти брокеру, коли робиш ставки на біржі? Про цінність математичного мислення і непомітні сторони діяльності брокера СТОРІНКА 96_
СНАРЯД. ЯКИЙ ЛЕТИТЬ
Рух по ПАРАБОЛІ, КВ. РІВНЯННЯ СТОРІНКА 104 -
НЕЗНАЧУЩІСТЬ ЗНАЧУЩОСТІ
Про контрацептиви та жінок. СТАТИСТИКА.
СТОРІНКА 115 -
МІФ ПРО МІФ ПРО СМУГУ УДАЧ
Баскетболісти, біржі. Чи можна постійно перемагати? ПРО ставлення до перемог і поразок, ПРО важливість рутинної роботи, навчання, тренування...
СТОРІНКА 119-
🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌🙌
Джерело: Фейсбук група Математика нова
Джерело: простори інтернету
!!!! Відео про викладача, який на першому уроці дістав літрову банку, наповнив її тенісними кульками, камінцями, піском і пивом. - Суть: у житті головне родина, здоров'я, любов, їх треба цінувати і опікуватися ними у першу чергу (це кульки тенісні), камінці - це рутина, тобто робота, хатні справи... Без них ніяк у житті. Вони завжди будуть у житті-банці. Пісок - це безліч того, що ми робимо, з чим зустрічаємося у житті, але те, що не є ні важливим, ні цінним. Іноді без нього можна обійтися. Так от будувати життя треба так, щоб важливі речі були в ньому на першому місці ( не пісок спочатку - бо кульки потім можуть і не поміститися!). А пиво до чого 😮? А пляшці пива завжди знайдеться місце у житті😁! Звісно , можна пиво замінити на воду чи колу!
😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉😉









Коментарі
Дописати коментар